本文为学习 Learning OpenCV 3 Computer vision in C++ 第4章的笔记。
这一章主要内容是介绍和使用 Mat 类,包含初始化,赋值 和元素遍历等内容。同时,也介绍了用于稀疏矩阵的 SparseMat 类。
引言
图像是由像素构成的——每个像素又可以有1、3或4个数值来表示,这样的形式适合用类似数组的数据结构来表示。在OpenCV中,使用 Mat 类来表示图像。但需要注意的是,Mat 本身可以用于实现任意维度的数组。在存在少量非零元素数组的场合,需要使用 SparseMat,这是一种和 Mat 类完全不一样的类。
在头文件的注释中,提供了很多示例,如 mat.hpp,可以用来上手实践。
Mat 类
Mat 类可以用于表示多维的数组,数组的元素可以是单通道,也可以是多通道的。用图像来说明的话,黑白图片就是单通道的,因为每个像素只需要使用1个数值就能表示;彩色图片是3通道的,因为每个像素需要使用RGB3种三原色来表示。
创建和初始化
创建 Mat 类数组的时候,需要指明维度,大小(size)和类型(元素的channel和数值类型)等等。因为二维数组是最常见的数组,有很多直接创建二维数组的构造函数,如:
cv::Mat m;
m.create(3, 10, CV_32FC3);
上述代码就是创建了一个3x10的二维数组,其元素类型是3通道的32位bit floats。
宏 CV_32FC3的阅读从下划线右开始,第一个数字表示数据类型的 bit数;紧跟着的字母表示某一个 premitive type,这里 f 表示 float;C表示channel;3则表示channel的数量。
使用 create(rows, cols, type) 是最常见的创建二维 Mat 方式之一。当需要创建多维时,经常使用的方式是 create(dims, size[], type) :
cv::Mat m;
m.create(3, [5, 5, 5], CV_32FC1);
这样是创建了一个三维的 5x5x5的单通道 float 数组。
创建完 Mat 实例可以使用set进行赋值, 如:
cv::Mat m;
m.create(3, 10, CV_32FC3);
m.setTo(Scalar(1.0f, 2.0f, 3.0f));
也可以在创建的时候就赋初值:
Mat M(7,7,CV_32FC2,Scalar(1,3));
还有一种使用二维数组来创建并初始化 mat 的方法,在作业部分,会使用到该方式。 假如有一个如下数组:
u_char f = 0xff;
u_char dataArray[3][10] = {
{0, 0, 0, 0, f, f, 0, 0, 0, 0},
{0, 0, 0, f, f, f, f, 0, 0, 0},
{0, 0, f, f, 0, 0, f, f, 0, 0},
}
可以使用如下方式生成相应的mat:
Mat mat = Mat(Size(10, 3), CV_8UC1, dataArray, sizeof(u_char) * 10);
注意,OpenCV中 Size 的构造函数是 Size (col,row)。
特殊的二维矩阵如全零/全一/单位矩阵,有相应的静态函数:
Mat::zeros(rows, cols, type);
Mat::ones(rows, cols, type);
Mat::eye(rows, cols, type);
注意:如果是多通道的类型,上述ones和eye静态函数只会作用于第一个通道,剩余通道值为0。
遍历与赋值
新版本的OpenCV推荐使用 at 和 iterator 进行元素的遍历。
at<>()
OpenCV 的C++版深度使用了模板,at函数也不例外。
m.at<premitive type>(row, col)
对于单通道 mat,上述就是类型为 premitive type 的数据。 若是多通道 mat,上述就是一个 vector 类型。比如:
Mat m = Mat::eye(5, 3, CV_8UC2);
m.at<u_char>(1,2)[0];
m.at<u_char>(1,2)[1];
迭代器 Iterator
MatIterator<> 和 MatConstIterator<> 是 Mat类内置的迭代器。
float a[][3] = {1.0f,2.0f,3.0f,4.0f,5.0f,6.0f,7.0f,8.0f,9.0f,10.0f,11.0f,12.0f,13.0f};
m = Mat(2, 2, CV_32FC3, a);
MatIterator_<Vec3f> m_begin = m.begin<Vec3f>();
MatIterator_<Vec3f> m_end = m.end<Vec3f>();
while (m_begin != m_end)
{
cout<< (*m_begin)[0]<<", "<<(*m_begin)[1]<<", "<<(*m_begin)[2]<<endl;
(*m_begin)[0] = 111;
m_begin++;
}
begin和end方法中需要指定type,书中不知道是否是印刷错误还是老版本的问题,缺少了
ptr
ptr方法是搜索的时候看到的,在书中第4章并没有提及,其用法如下:
for(int i = 0; i < m.rows; i ++) {
float *ptr = m.ptr<float>(i);
for (int j = 0; j < m.cols*m.channels(); j++)
{
cout<<"("<<i<<","<<j<<"):"<<(float)ptr[j]<<" ";
}
cout<<endl;
}
NAryMatIterator
前述Iterator是 Mat类的内置迭代器,它迭代的是 mat 实例的元素。NAryMatIterator 迭代的是具有相同维度的数组。在这里有一个 plane 的概念,指的是输入数组的一部分(通常是一维或者二维的切片)并且在内存中是连续的。它既可以用于高维数组,又能用于多个具有相同维度的数组。 Exercise4-1和 Exercise4-2 分别展示了这两种用途。
Exercise4-1: iterate high dims mat
//exercise4-1: iterate high dims mat
const int n_mat_size = 5;
const int n_mat_sz[] = {n_mat_size, n_mat_size, n_mat_size};
Mat n_mat(3, n_mat_sz, CV_32FC1);
RNG rng;
rng.fill(n_mat, RNG::UNIFORM, 0.f, 1.f);
const Mat* arrays[] = {&n_mat, 0};
Mat my_planes[1];
NAryMatIterator it(arrays, my_planes);
float s = 0.f;
int n = 0;
cout<<"nplanes:"<<it.nplanes<<endl<<"narrays:"<<it.narrays<<endl;
for (int p = 0; p < it.nplanes; p++, ++it)
{
cout<<it.planes[0]<<endl;
cout<<"tmp:"<<sum(it.planes[0])<<endl;
s += sum(it.planes[0])[0];
n ++;
}
cout<<"s:"<<s<<endl;
exercise4-2: iterate multiple mats
//exercise4-2: iterate multiple mats
const int n_mat_size = 5;
const int n_mat_sz[] = {n_mat_size, n_mat_size, n_mat_size};
Mat n_mat0(3, n_mat_sz, CV_32FC1);
Mat n_mat1(3, n_mat_sz, CV_32FC1);
RNG rng;
rng.fill(n_mat0, RNG::UNIFORM, 0.f, 1.f);
rng.fill(n_mat1, RNG::UNIFORM, 0.f, 1.f);
const Mat* arrays[] = {&n_mat0, &n_mat1, 0};
Mat my_planes[2];
NAryMatIterator it(arrays, my_planes);
float s= 0.f;
int n = 0;
cout<<"nplanes:"<<it.nplanes<<endl;
for(int p = 0; p < it.nplanes; p++, ++it) {
cout<<"plane[0]:"<<it.planes[0]<<endl;
cout<<"plane[1]:"<<it.planes[1]<<endl;
s+= sum(it.planes[0])[0];
s+= sum(it.planes[1])[0];
n++;
}
cout<<"n:"<<n<<endl;
访问子集
顾名思义,就是访问某一行,某一列,某个Range——rowRange,colRange,某个矩形等。需要特别注意的是,这样方法返回的是指针,并没有将内存的值重新复制。如果需要将某个 Mat 的部分数据复制到新的 Mat,需要使用 clone 或 copyTo 方法。
Saturation Casting
saturate_cast<>是在做操作的时候,设置元素的取值范围,作用是防止溢出。比如对于uchar取值是在 0~128。如果数值小于0,则返回0;如果数值大于128,则返回128。
SpartMat 类
稀疏矩阵除了在线性代数中会遇到外,在OpenCV中计算直方图,表示高维数组时也有使用,其C++实现是 SparseMat。SparseMat 只将非零元素存储在连续的内存中,这样可以节省空间。背后的实现是使用了 hash 表来存储非零元素。通过位置来生成 hash key,再通过 hash key 来获取 value。
SpartMat 的用法:
int size[] = {10, 10};
SparseMat sm(2, size, CV_32F);
for (int i = 0; i < 10; i++)
{
int idx[2];
idx[0] = size[0] * rand();
idx[1] = size[1] * rand();
printf("%d, %d\n", idx[0], idx[1]);
sm.ref<float>(idx) += 1.0f;
}
SparseMatConstIterator_<float> it = sm.begin<float>();
SparseMatConstIterator_<float> it_end = sm.end<float>();
for (; it != it_end; it++)
{
const SparseMat::Node* node = it.node();
printf("(%3d, %3d) %f\n", node->idx[0], node->idx[1], *it);
}
大型数组类型的模板结构
第3章基本数据类型就介绍了OpenCV C++中大量使用了 template,比如 Point2f, 其本质 Point2f是一个宏:
typedef Point_<float> Point2f;
Point_template<typename _Tp> class Point_ 模板类声明的。
而Mat_<>有一些不一样,它是继承自 Mat,如:
template<typename _Tp> class Mat_ : public Mat
这样的好处是什么? 尤其是 Mat 类的构造函数可以通过 type 指定,从而可以存储任意数据类型的时候。注意,当使用 Mat 实例的 at 或 begin 等成员函数的时候,是需要带上
作业
作业1
作业1的主要内容是:
- 创建一个500x500 的区域,区域内单通道并初始化每个元素为0;
- 输入数字,在区域内显示,每个数字大小 10 x 20;
- 从左往右输入,到到区域右侧后,即使有输入也不再显示;
- 支持删除和换行,还可以通过左右上下键进行编辑;
- 输入某个键,支持将图像切换到彩色,每一个数字有其独特的颜色;
我一开始搜索了下,发现有 putText API,后来才意识到并不需要使用API来实现。对于单通道 uchar 类型的图片来说,0 表示黑,255 表示白。通过对 500x500 的区域内的子区域进行局部赋值,可以实现数字的显示。因此需要知道:
- 如何显示数字;
- 如何局部赋值;
第一个小问题,可以使用上述使用二维数组来创建并初始化 mat 的方法,比如说数字2可以:
u_char f = 0xff;
u_char twoArrays[20][10] = {
{0, 0, 0, 0, f, f, 0, 0, 0, 0},
{0, 0, 0, f, f, f, f, 0, 0, 0},
{0, 0, f, f, 0, 0, f, f, 0, 0},
{0, f, f, 0, 0, 0, 0, f, f, 0},
{f, f, 0, 0, 0, 0, 0, 0, f, f},
{f, 0, 0, 0, 0, 0, 0, 0, f, f},
{0, 0, 0, 0, 0, 0, 0, f, f, 0},
{0, 0, 0, 0, 0, 0, 0, f, f, 0},
{0, 0, 0, 0, 0, 0, f, f, 0, 0},
{0, 0, 0, 0, 0, f, f, 0, 0, 0},
{0, 0, 0, 0, f, f, 0, 0, 0, 0},
{0, 0, 0, 0, f, f, 0, 0, 0, 0},
{0, 0, 0, f, f, 0, 0, 0, 0, 0},
{0, 0, 0, f, f, 0, 0, 0, 0, 0},
{0, 0, f, f, 0, 0, 0, 0, 0, 0},
{0, 0, f, f, 0, 0, 0, 0, 0, 0},
{0, f, f, 0, 0, 0, 0, 0, 0, 0},
{f, f, 0, 0, 0, 0, 0, 0, 0, 0},
{f, f, f, f, f, f, f, f, f, f},
{f, f, f, f, f, f, f, f, f, f}
};
Mat mat2 = Mat(Size(10, 20), CV_8UC1, twoArrays, sizeof(u_char) * 10);
因此,预先创建 0~9 的二维数组,再创建相应的 mat,留作后用。
第二个问题就使用 copyTo方法:
//i: row, j: col
mat2.copyTo(mat(Range(j * 20, j *20 + 20), Range((i - 1) * 10, (i - 1)*10 + 10)));
至于回车,删除和上下左右移动就是检测键盘输入,并根据输入的 ASCII 值进行判断,大致逻辑:
while (true)
{
auto keyPress = waitKey(20);
if (-1 != keyPress)
{
cout << "keyPress:" << keyPress << endl;
}
switch (keyPress) {
//
}
}
如果需要转换成彩色图像的话,原理也是类似。每个数字使用三通道mat表示,注意颜色顺序的BGR。
因为没有完成所有步骤,就不贴代码了。
作业2
积分图像 Integral Image
作业2是求解 integral image 积分图像。积分图像的定义是一个和原始图像相同维度的新mat中,每个元素是当前位置到原始图像左上角区域内的所有元素之和。示例,原始图像为:
1 2 3 4 5
6 7 8 9 10
那对应的积分图像为:
1 3 6 10 15
7 16 27 40 55
按照定义计算的时候,要注意复用已经计算过的区域,比如计算如下 ?位置的积分值:
1 3 6 10 15
7 16 ?
可以使用 8 + 16 + 6 - 3 = 27 得出。这个公式可以抽象为:? = 原?处的值 + A + B - C ——画个图很容易得出该结论。
x x x x x
x x C B x
x x A ?
按照定义来实现的时候,第一个、第一行和第一列的积分值要特殊处理:
for(int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if(0 == i && 0 == j) {
mat_integral2.at<float>(i, j) = mat_uchar.at<uchar>(i, j);
}else if (0 == i && 0 != j) {
mat_integral2.at<float>(i, j) = mat_integral2.at<float>(i, j - 1) + mat_uchar.at<uchar>(i, j);
}else if (0 != i && 0 == j) {
mat_integral2.at<float>(i, j) = mat_integral2.at<float>(i - 1, j) + mat_uchar.at<uchar>(i, j);
}else {
mat_integral2.at<float>(i, j) = mat_integral2.at<float>(i, j - 1) + mat_integral2.at<float>(i - 1, j) - mat_integral2.at<float>(i - 1, j - 1) + mat_uchar.at<uchar>(i, j);
}
}
}
但参考链表中的 dummy node 实现,如果在第一行之上添加一行0并在第一列左边添加一列0,这样就可以通过一个循环把包含特殊位置(第一行和第一列)的所有元素的积分值求出了:
Mat mat_integral = Mat::zeros(Size(cols+1, rows+1), CV_32FC1);
for(int i = 1; i < rows + 1; i++) {
for (int j = 1; j < cols + 1; j++) {
mat_integral.at<float>(i, j) = mat_integral.at<float>(i, j - 1) + mat_integral.at<float>(i - 1, j) - mat_integral.at<float>(i - 1, j - 1) + mat_uchar.at<uchar>(i - 1, j - 1);
}
}
OpenCV中的 API integral 的输入参数中也是传入 Size(cols+1, rows+1) 的目标 mat。
利用积分图像,可以在常数时间内快速地算出原始图像中的任意矩形内的 sum 值。例如求解下图中矩形ABCD的积分值,可以使用:
Sum(ABCD) = I(C)-I(d)-I(b)+I(a) 求得。
其中,a,b,d分别指的是邻近的积分值。
------------------------------------->x
|
|
| b
| aA--------B
| | |
| | |
| dD--------C
|
|
↓
y
旋转积分图像 Tiled Integral Image
这里的旋转特指45度的旋转,以下图为例(此图来自 matlab的官方文档):
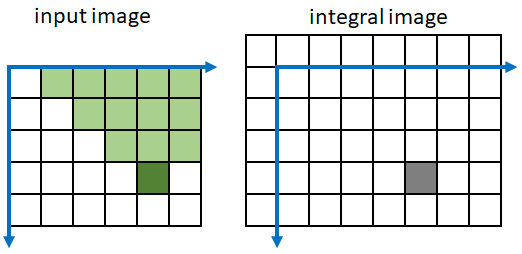
左边是已旋转的原始图像,深绿色点的积分值在右图的灰色处,其计算是将对角线内的所有像素点求和。
你可以这样理解旋转积分图像:把(未旋转的)正常的图像点和坐标轴,整体顺时针旋转45度,—— 这样就能理解上述所说对角线内的所有像素之和了。
此时灰色点的值可以参照下图计算:
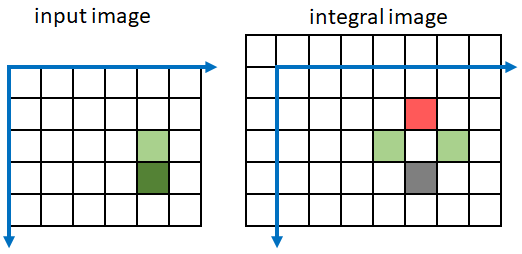
其公式为: J(m,n) = J(m-1,n-1) + J(m-1,n+1) - J(m-2,n) + I(m-1,n-1) + I(m-2,n-1)。
注意,matlab 中 m 为向下的坐标轴,n 为向右的坐标轴。
求解旋转图像内某个区域的积分值的方法和
Comments